- Agent & Environment Interface: At each step t the agent receives a state S_t, performs an action A_t and receives a reward R_{t+1}. The action is chosen according to a policy function pi.
- The total return G_t is the sum of all rewards starting from time t . Future rewards are discounted at a discount rate gamma^k.
- Markov property: The environment's response at time t+1 depends only on the state and action representations at time t. The future is independent of the past given the present. Even if an environment doesn't fully satisfy the Markov property we still treat it as if it is and try to construct the state representation to be approximately Markov.
- Markov Decision Process (MDP): Defined by a state set S, action set A and one-step dynamics p(s',r | s,a). If we have complete knowledge of the environment we know the transition dynamic. In practice, we often don't know the full MDP (but we know that it's some MDP).
- The Value Function v(s) estimates how "good" it is for an agent to be in a particular state. More formally, it's the expected return G_t given that the agent is in state s. v(s) = Ex[G_t | S_t = s]. Note that the value function is specific to a given policy pi.
- Action Value function: q(s, a) estimates how "good" it is for an agent to be in states and take action a. Similar to the value function, but also considers the action.
- The Bellman equation expresses the relationship between the value of a state and the values of its successor states. It can be expressed using a "backup" diagram. Bellman equations exist for both the value function and the action value function.
- Value functions define an ordering over policies. A policy p1 is better than p2 if v_p1(s) >= v_p2(s) for all states s. For MDPs, there exist one or more optimal policies that are better than or equal to all other policies.
- The optimal state value function v*(s) is the value function for the optimal policy. Same for q*(s, a). The Bellman Optimality Equation defines how the optimal value of a state is related to the optimal value of successor states. It has a "max" instead of an average.
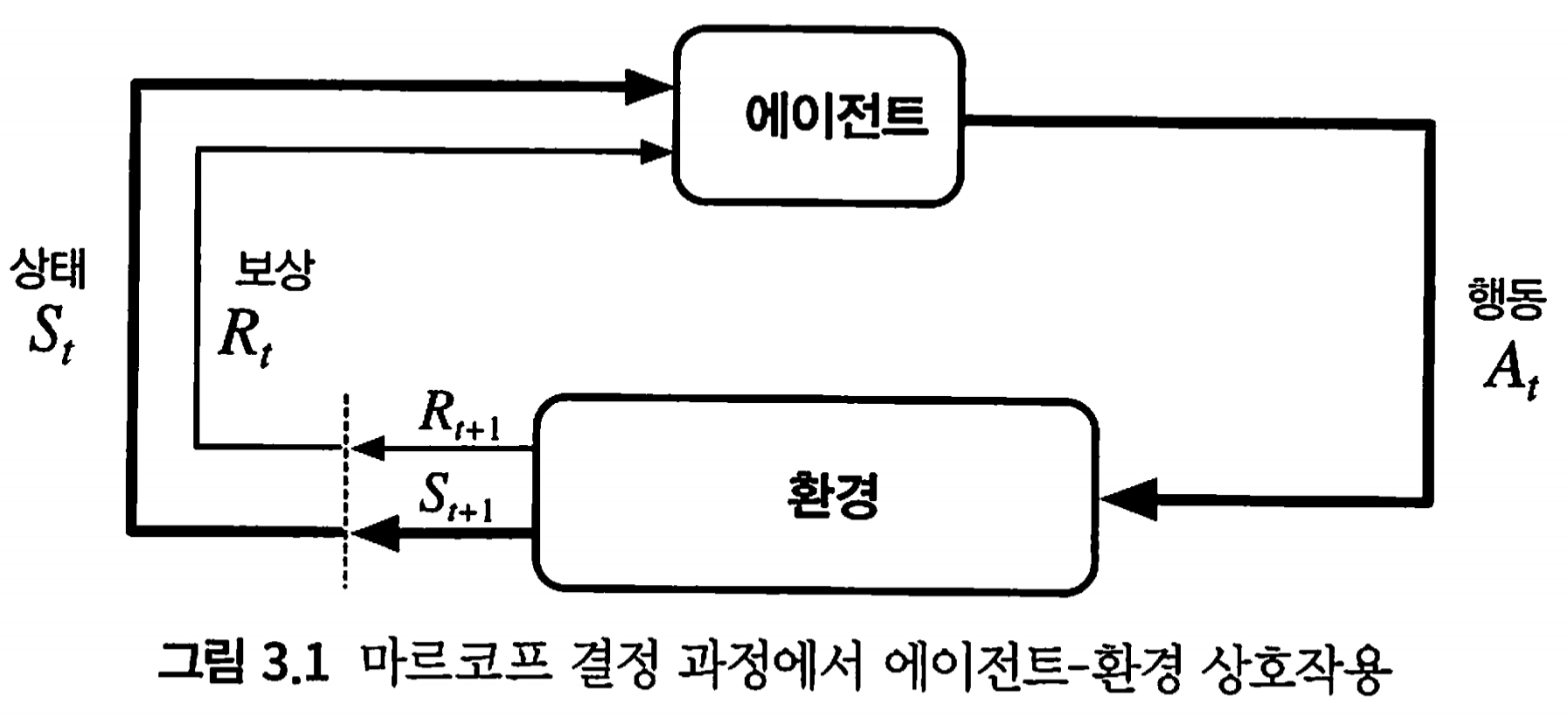
그러므로 agent는 다음과 같은 state, action, reward의 나열을 경험하며 이를 trajectory라고 부른다고 함

p(s’, r | s, a)는 state s에서 action a를 취했을 때 그 다음 state가 s’이 되고 받는 reward가 r이 될 확률임
주의할 점은 받는 reward r이 s’에 도달하여 일대일로 정해지는 값이 아니고 확률적으로 r을 받는 구조임.

강화학습이 최대화하려는 목표값은 reward가 아닌 G_t임. <- 누적 보상합

policy pi하에 state s의 가치를 매기는 함수 v_pi (state-value function for policy pi)
최종 상태의 reward는 항상 0

policy pi하에 state s에서 취하는 action a의 가치를 매기는 함수 q_pi(s, a) (action-value function for policy pi)

벨만 방정식 (Bellman eqn)
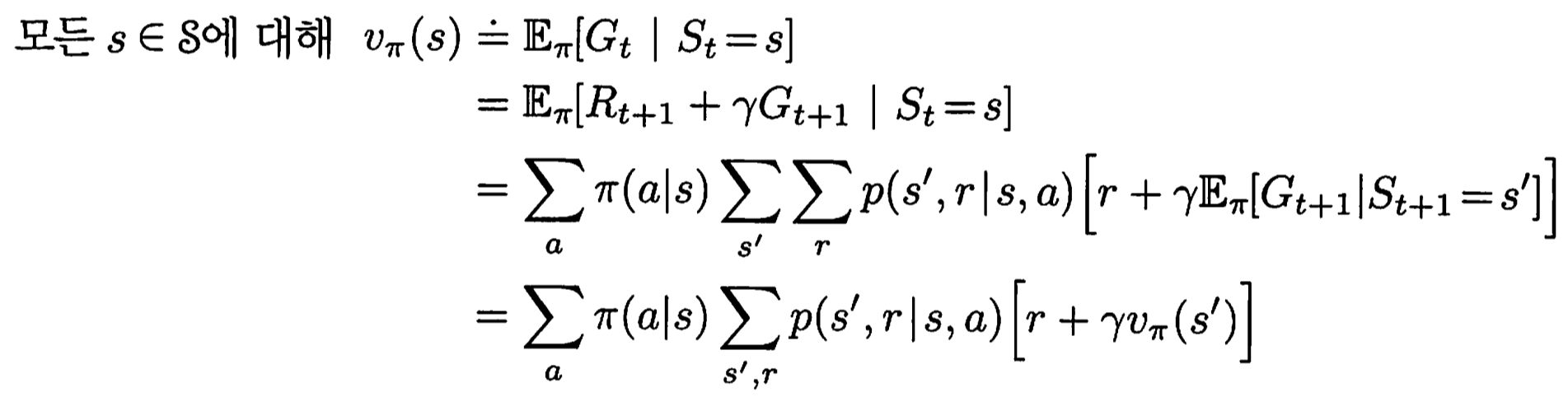

최적 상태 가치 함수 (optimal state-value function)

최적 행동 가치 함수 (optimal action-value function)


최적 벨만 방정식 (Bellman optimality eqn)

'Reinforcement Learning' 카테고리의 다른 글
| Introduction (2) | 2023.01.21 |
|---|---|
| dennybritz/reinforcement-learning (0) | 2023.01.21 |
- Agent & Environment Interface: At each step t the agent receives a state S_t, performs an action A_t and receives a reward R_{t+1}. The action is chosen according to a policy function pi.
- The total return G_t is the sum of all rewards starting from time t . Future rewards are discounted at a discount rate gamma^k.
- Markov property: The environment's response at time t+1 depends only on the state and action representations at time t. The future is independent of the past given the present. Even if an environment doesn't fully satisfy the Markov property we still treat it as if it is and try to construct the state representation to be approximately Markov.
- Markov Decision Process (MDP): Defined by a state set S, action set A and one-step dynamics p(s',r | s,a). If we have complete knowledge of the environment we know the transition dynamic. In practice, we often don't know the full MDP (but we know that it's some MDP).
- The Value Function v(s) estimates how "good" it is for an agent to be in a particular state. More formally, it's the expected return G_t given that the agent is in state s. v(s) = Ex[G_t | S_t = s]. Note that the value function is specific to a given policy pi.
- Action Value function: q(s, a) estimates how "good" it is for an agent to be in states and take action a. Similar to the value function, but also considers the action.
- The Bellman equation expresses the relationship between the value of a state and the values of its successor states. It can be expressed using a "backup" diagram. Bellman equations exist for both the value function and the action value function.
- Value functions define an ordering over policies. A policy p1 is better than p2 if v_p1(s) >= v_p2(s) for all states s. For MDPs, there exist one or more optimal policies that are better than or equal to all other policies.
- The optimal state value function v*(s) is the value function for the optimal policy. Same for q*(s, a). The Bellman Optimality Equation defines how the optimal value of a state is related to the optimal value of successor states. It has a "max" instead of an average.

그러므로 agent는 다음과 같은 state, action, reward의 나열을 경험하며 이를 trajectory라고 부른다고 함

p(s’, r | s, a)는 state s에서 action a를 취했을 때 그 다음 state가 s’이 되고 받는 reward가 r이 될 확률임
주의할 점은 받는 reward r이 s’에 도달하여 일대일로 정해지는 값이 아니고 확률적으로 r을 받는 구조임.

강화학습이 최대화하려는 목표값은 reward가 아닌 G_t임. <- 누적 보상합

policy pi하에 state s의 가치를 매기는 함수 v_pi (state-value function for policy pi)
최종 상태의 reward는 항상 0

policy pi하에 state s에서 취하는 action a의 가치를 매기는 함수 q_pi(s, a) (action-value function for policy pi)

벨만 방정식 (Bellman eqn)
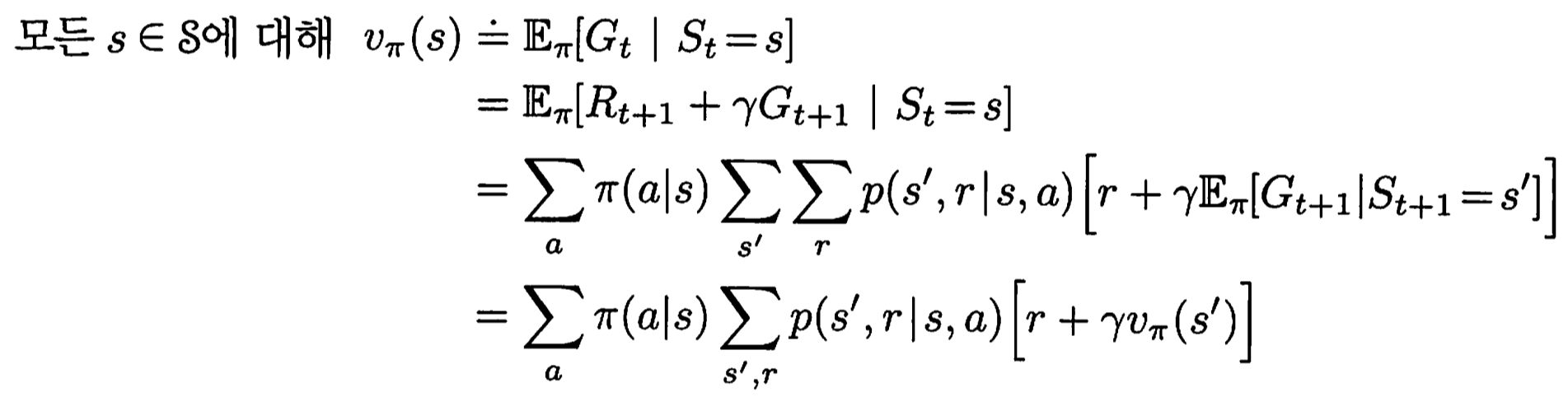

최적 상태 가치 함수 (optimal state-value function)

최적 행동 가치 함수 (optimal action-value function)


최적 벨만 방정식 (Bellman optimality eqn)

'Reinforcement Learning' 카테고리의 다른 글
| Introduction (2) | 2023.01.21 |
|---|---|
| dennybritz/reinforcement-learning (0) | 2023.01.21 |
