Stochastic Gradient Descent & Mini-Batch Gradient Descent

출처

딥러닝 CNN 완벽 가이드 - Fundamental 편

https://www.inflearn.com/course/%EB%94%A5%EB%9F%AC%EB%8B%9D-cnn-%EC%99%84%EB%B2%BD-%EA%B8%B0%EC%B4%88

딥러닝 CNN 완벽 가이드 - Fundamental 편 - 인프런 | 강의

이론

Gradient Descent는 전체 학습 데이터를 기반으로 weight와 bias를 업데이트 함

근데 입력 데이터 많아지고 네트워크 레이어가 깊어질수록 일반적인 GD를 하기에 계산량이 너무 많음

 

SGD : 전체 학습 데이터 중에서 한 건만 GD 적용

Mini-Batch GD : 전체 학습 데이터 중에서 batch 크기만큼 GD 적용 (← 일반적으로 쓰임)

 

이렇게 두 가지 해결 방안이 도입됨

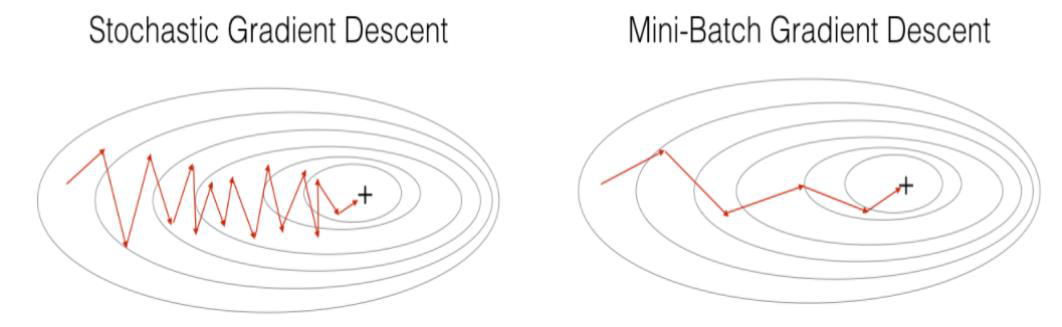
↓ Mini-Batch 방식에는 두 가지가 있음

첫 번째 방식은 epoch 한 번에 batch_size만큼 100개만 골라서 GD 학습

두 번째 방식은 epoch 한 번에 batch_size만큼 100개 고른 후 GD 학습 적용하는 절차를

4번 시행해서 전체 학습 데이터를 훑어봄

실습

Stochasic Gradient Descent

https://tomorrow-study.tistory.com/6 

Gradient Descent

랑 거의 유사한 코드 사용함

import numpy as np
import pandas as pd
from sklearn.datasets import load_boston

boston = load_boston()
bostonDF = pd.DataFrame(data=boston['data'], columns=boston['feature_names'])
bostonDF['PRICE'] = boston['target']

↓ weight/bias update value 구하는 함수 구현

sgd는 하나의 데이터에 대해 weight/bias를 업데이트하기 때문에 loss는 아래에서 작성

def get_descent_values_sgd(w1, w2, bias, rm_sgd, lstat_sgd, price_sgd, learning_rate=.01):
    N = price_sgd.shape[0] # N = 1
    pred_sgd = w1 * rm_sgd + w2 * lstat_sgd + bias
    diff_sgd = price_sgd - pred_sgd
    
    dw1 = learning_rate * (2 / N) * (diff_sgd * rm_sgd)
    dw2 = learning_rate * (2 / N) * (diff_sgd * lstat_sgd)
    db = learning_rate * (2 / N) * diff_sgd
    # loss = np.mean(np.square(diff))
    
    return dw1, dw2, db

↓ sgd 구현하는 함수

여기서 loss는 전체 학습 데이터 기반으로 구해야 함

def stochastic_gradient_descent(features, price, epochs, verbose=True):
    np.random.seed = 2023
    
    w1 = np.zeros((1,))
    w2 = np.zeros((1,))
    bias = np.ones((1,))
    print('#' * 15 + ' initial weights ' + '#' * 15)
    print('w1', w1, 'w2', w2, 'bias', bias)
    print('#' * 47)
    print()
    
    learning_rate = .01
    rm = features[:, 0]
    lstat = features[:, 1]
    
    for i in range(epochs):
        stoch_idx = np.random.choice(price.shape[0], 1) # 1개 random choice
        rm_sgd = rm[stoch_idx]
        lstat_sgd = lstat[stoch_idx]
        price_sgd = price[stoch_idx]
        
        dw1, dw2, db = get_descent_values_sgd(w1, w2, bias, rm_sgd, lstat_sgd, price_sgd, learning_rate)
        w1 += dw1
        w2 += dw2
        bias += db
        
        if verbose:
            print('Epoch :', i + 1, '/', epochs)
            
            pred = w1 * rm + w2 * lstat + bias
            diff = price - pred
            loss = np.mean(np.square(diff))
            
            print('w1', w1, 'w2', w2, 'bias', bias, 'loss', loss)
    
    return w1, w2, bias

↓ 정규화 (MinMaxScaler)

from sklearn.preprocessing import MinMaxScaler

scaler = MinMaxScaler()
scaled_features = scaler.fit_transform(bostonDF[['RM', 'LSTAT']])

↓ epoch 5000으로 SGD 학습

w1, w2, bias = stochastic_gradient_descent(scaled_features, bostonDF['PRICE'].values, epochs=5000, verbose=True)

print()
print('#' * 15 + ' final weights ' + '#' * 15)
print('w1', w1, 'w2', w2, 'bias', bias)
print('#' * 45)

↓ 결과

############### initial weights ###############
w1 [0.] w2 [0.] bias [1.]
###############################################

Epoch : 1 / 5000
w1 [0.19708373] w2 [0.1080894] bias [1.372] loss 526.4361550859163
Epoch : 2 / 5000
w1 [0.22427674] w2 [0.35405183] bias [1.61796243] loss 513.1031266790037
Epoch : 3 / 5000
w1 [0.28758114] w2 [0.42592688] bias [1.75585294] loss 505.25474719185155
Epoch : 4 / 5000
w1 [0.49101408] w2 [0.53724563] bias [2.16961618] loss 482.8198923681914
Epoch : 5 / 5000
w1 [0.64487981] w2 [0.66989593] bias [2.47253028] loss 466.21121010236527
Epoch : 6 / 5000
w1 [1.40872988] w2 [0.67482418] bias [3.41252875] loss 414.39640931621295
Epoch : 7 / 5000
w1 [1.4594593] w2 [0.75119601] bias [3.55728372] loss 407.4893404612513
Epoch : 8 / 5000
w1 [1.60366032] w2 [0.88502813] bias [3.93151799] loss 390.22308414795094
Epoch : 9 / 5000
w1 [1.81168404] w2 [0.93463169] bias [4.32573578] loss 372.1553417938602
Epoch : 10 / 5000
w1 [1.97662038] w2 [0.9968901] bias [4.66198686] loss 357.2601545165384

...

Epoch : 4991 / 5000
w1 [25.78137533] w2 [-22.27755829] bias [16.7720665] loss 31.54811228195822
Epoch : 4992 / 5000
w1 [25.74287932] w2 [-22.2859494] bias [16.69183062] loss 31.35880620386689
Epoch : 4993 / 5000
w1 [25.79896847] w2 [-22.23751593] bias [16.83511463] loss 31.723410428851956
Epoch : 4994 / 5000
w1 [25.87009501] w2 [-22.22733327] bias [16.94461593] loss 32.06089016727292
Epoch : 4995 / 5000
w1 [25.88679124] w2 [-22.22580726] bias [16.96866053] loss 32.14174505598724
Epoch : 4996 / 5000
w1 [25.89856411] w2 [-22.21652605] bias [16.9952706] loss 32.23189462923306
Epoch : 4997 / 5000
w1 [25.95911543] w2 [-22.18354463] bias [17.08679024] loss 32.590624895422145
Epoch : 4998 / 5000
w1 [25.93725451] w2 [-22.19691084] bias [17.03674982] loss 32.40949512101921
Epoch : 4999 / 5000
w1 [25.90763075] w2 [-22.21667166] bias [16.97927533] loss 32.20247951845019
Epoch : 5000 / 5000
w1 [25.86119595] w2 [-22.23779962] bias [16.88833978] loss 31.908978775718037

############### final weights ###############
w1 [25.86119595] w2 [-22.23779962] bias [16.88833978]
#############################################

GD와의 차이점은 GD의 loss는 항상 단조감소하는 반면, SGD의 loss는 대체로 감소하는 경향을 보이지만 이따금 값이 커지기도 한다.

 

이전에 GD로 구현했을 때는

Epoch : 5000 / 5000
w1 [25.41862187] w2 [-23.60046384] bias [16.38568321] loss 30.52907816250869

인데 GD가 SGD보다 더 loss가 적다 (엥)

pred_price = scaled_features[:, 0] * w1 + scaled_features[:, 1] * w2 + bias
bostonDF['PRED_PRICE_SGD'] = pred_price
bostonDF

Mini-Batch Gradient Descent (Random, 첫 번째 방식)

↓ weight/bias update value 구하는 함수 구현

batch gd는 batch_size만큼의 데이터에 대해 weight/bias를 업데이트하기 때문에 loss는 아래에서 작성

def get_descent_values_batch(w1, w2, bias, rm_batch, lstat_batch, price_batch, learning_rate=.01):
    N = price_batch.shape[0]
    pred_batch = w1 * rm_batch + w2 * lstat_batch + bias
    diff_batch = price_batch - pred_batch
    
    dw1 = learning_rate * (2 / N) * (diff_batch @ rm_batch)
    dw2 = learning_rate * (2 / N) * (diff_batch @ lstat_batch)
    db = learning_rate * (2 / N) * sum(diff_batch)
    # loss = np.mean(np.square(diff))
    
    return dw1, dw2, db

↓ Mini-Batch GD 구현하는 함수

여기서 loss는 전체 학습 데이터 기반으로 구해야 함

def batch_random_gradient_descent(features, price, epochs, batch_size, verbose=True):
    np.random.seed = 2023
    
    w1 = np.zeros((1, ))
    w2 = np.zeros((1, ))
    bias = np.ones((1, ))
    
    print('#' * 15 + ' initial weights ' + '#' * 15)
    print('w1', w1, 'w2', w2, 'bias', bias)
    print('#' * 47)
    print()
    
    learning_rate = .01
    rm = features[:, 0]
    lstat = features[:, 1]
    
    for i in range(epochs):
        batch_idx = np.random.choice(price.shape[0], batch_size) # batch_size만큼 random choice
        rm_batch = rm[batch_idx]
        lstat_batch = lstat[batch_idx]
        price_batch = price[batch_idx]
        
        dw1, dw2, db = get_descent_values_batch(w1, w2, bias, rm_batch, lstat_batch, price_batch, learning_rate)
        w1 += dw1
        w2 += dw2
        bias += db
        
        if verbose:
            print('Epoch :', i + 1, '/', epochs)
            
            pred = w1 * rm + w2 * lstat + bias
            diff = price - pred
            loss = np.mean(np.square(diff))
            
            print('w1', w1, 'w2', w2, 'bias', bias, 'loss', loss)
    
    return w1, w2, bias

↓ epoch 5000으로 Mini-Batch GD 학습

batch_size는 30으로 입력했음

w1, w2, bias = batch_random_gradient_descent(scaled_features, bostonDF['PRICE'].values, epochs=5000, batch_size=30, verbose=True)

print()
print('#' * 15 + ' final weights ' + '#' * 15)
print('w1', w1, 'w2', w2, 'bias', bias)
print('#' * 45)

↓ 결과

############### initial weights ###############
w1 [0.] w2 [0.] bias [1.]
###############################################

Epoch : 1 / 5000
w1 [0.25840625] w2 [0.09566181] bias [1.46713333] loss 521.1244917182498
Epoch : 2 / 5000
w1 [0.52737613] w2 [0.18631768] bias [1.89820818] loss 496.23429251462625
Epoch : 3 / 5000
w1 [0.72263093] w2 [0.27758874] bias [2.28505848] loss 475.4481533604007
Epoch : 4 / 5000
w1 [1.01989237] w2 [0.36253845] bias [2.75694231] loss 449.7691345912719
Epoch : 5 / 5000
w1 [1.21937111] w2 [0.44370448] bias [3.12912893] loss 430.7355651013831
Epoch : 6 / 5000
w1 [1.400479] w2 [0.54207252] bias [3.47146244] loss 413.5246482041456
Epoch : 7 / 5000
w1 [1.59539808] w2 [0.62862252] bias [3.83366921] loss 395.8629747357811
Epoch : 8 / 5000
w1 [1.76332031] w2 [0.70618069] bias [4.14956013] loss 380.8772068513673
Epoch : 9 / 5000
w1 [2.0154502] w2 [0.78663443] bias [4.5519081] loss 361.7237091959738
Epoch : 10 / 5000
w1 [2.19861225] w2 [0.86939646] bias [4.88637362] loss 346.6558477105803

...

Epoch : 4991 / 5000
w1 [25.35578208] w2 [-23.65392409] bias [16.56233288] loss 30.547955573240788
Epoch : 4992 / 5000
w1 [25.35268203] w2 [-23.65116937] bias [16.55791945] loss 30.54673703595858
Epoch : 4993 / 5000
w1 [25.33372557] w2 [-23.6659809] bias [16.51728346] loss 30.536225836681005
Epoch : 4994 / 5000
w1 [25.34006871] w2 [-23.6633483] bias [16.52114633] loss 30.53726058568498
Epoch : 4995 / 5000
w1 [25.36300697] w2 [-23.65799674] bias [16.55542924] loss 30.546542759888403
Epoch : 4996 / 5000
w1 [25.36430521] w2 [-23.66783969] bias [16.55096792] loss 30.544718633419144
Epoch : 4997 / 5000
w1 [25.35759863] w2 [-23.67382728] bias [16.54094673] loss 30.541390684985853
Epoch : 4998 / 5000
w1 [25.35999356] w2 [-23.6818518] bias [16.54269226] loss 30.541364623196845
Epoch : 4999 / 5000
w1 [25.35436669] w2 [-23.68213233] bias [16.53456573] loss 30.53928792114059
Epoch : 5000 / 5000
w1 [25.34313455] w2 [-23.69338227] bias [16.51080747] loss 30.5343362125283

############### final weights ###############
w1 [25.34313455] w2 [-23.69338227] bias [16.51080747]
#############################################

확실히 SGD보다 빠르게 GD의 loss 값으로 수렴한다

SGD는 하나의 데이터만 반영했지만 Mini-Batch GD는 30개 데이터를 반영해서 뭉탱이로 반영했기 때문

그리고 SGD처럼 loss값 변동 폭이 크지 않고 안정적으로 수렴함

Mini-Batch Gradient Descent (전체 학습 데이터, 두 번째 방식)