출처
딥러닝 CNN 완벽 가이드 - Fundamental 편
딥러닝 CNN 완벽 가이드 - Fundamental 편 - 인프런 | 강의
딥러닝·CNN 핵심 이론부터 다양한 CNN 모델 구현 방법, 실전 문제를 통한 실무 딥러닝 개발 노하우까지, 딥러닝 CNN 기술 전문가로 거듭나고 싶다면 이 강의와 함께하세요 :), - 강의 소개 | 인프런..
www.inflearn.com
이론

mse loss function 그래프에서 점진적인 하강을 통해 local minimum/maximum을 찾아나가는 방식
mse loss function 기울기에 learning_rate를 곱해서 weight/bias를 업데이트함
↑ 각 weight/bias로 편미분해서 기울기를 구함
보스턴 주택 가격 데이터 세트 학습 실습
뉴럴 네트워크 직접 구현
import numpy as np
import pandas as pd
from sklearn.datasets import load_boston
boston = load_boston()
print(boston['feature_names'])['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO' 'B' 'LSTAT']여러 features 중에서 영향력이 제일 큰 RM과 LSTAT만 이용해 예측해 봄
bostonDF = pd.DataFrame(data=boston['data'], columns=boston['feature_names'])
bostonDF['PRICE'] = boston['target']
bostonDF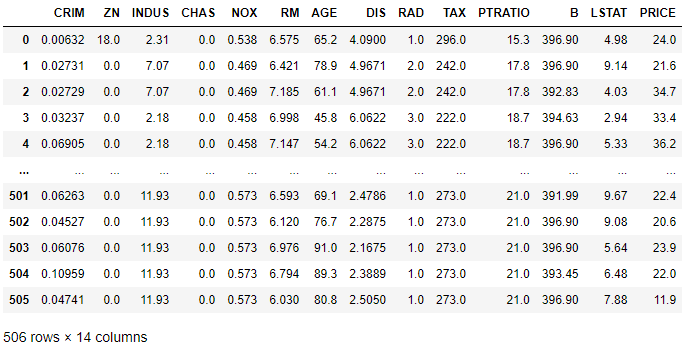
↓ 뉴럴 네트워크 구조
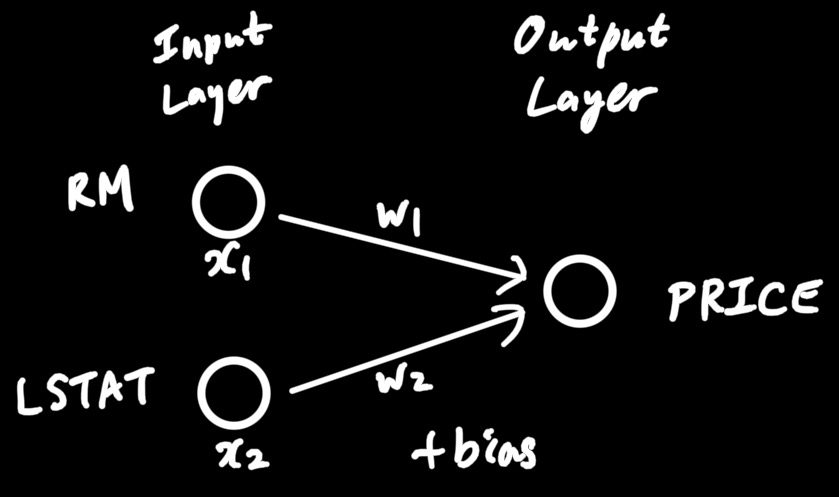
↓ Gradient Descent 원리

↓ weight/bias update value 구하는 함수 구현
def get_descent_values(w1, w2, bias, rm, lstat, price, learning_rate=.01):
N = len(price)
pred = w1 * rm + w2 * lstat + bias
diff = price - pred
dw1 = learning_rate * (2 / N) * (diff @ rm)
dw2 = learning_rate * (2 / N) * (diff @ lstat)
db = learning_rate * (2 / N) * sum(diff)
loss = np.mean(np.square(diff))
return dw1, dw2, db, loss↑ 여기서 rm, lstat, price는 모두 1차원 배열 형태로 입력될 예정
↓ 드디어 gradient descent 구현하는 함수
def gradient_descent(features, price, epochs, verbose=True):
w1 = np.zeros((1,))
w2 = np.zeros((1,))
bias = np.ones((1,))
print('#' * 15 + ' initial weights ' + '#' * 15)
print('w1', w1, 'w2', w2, 'bias', bias)
print('#' * 47)
print()
learning_rate = .01
rm = features[:, 0]
lstat = features[:, 1]
for i in range(epochs):
dw1, dw2, db, loss = get_descent_values(w1, w2, bias, rm, lstat, price, learning_rate)
w1 += dw1
w2 += dw2
bias += db
if verbose:
print('Epoch :', i + 1, '/', epochs)
print('w1', w1, 'w2', w2, 'bias', bias, 'loss', loss)
return w1, w2, bias데이터에 preprocessing이 필요함
↓ 보통 데이터를 0에서 1 사이로 정규화해 놓는 게 좋음
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaled_features = scaler.fit_transform(bostonDF[['RM', 'LSTAT']])
print(scaled_features[:10])[[0.57750527 0.08967991]
[0.5479977 0.2044702 ]
[0.6943859 0.06346578]
[0.65855528 0.03338852]
[0.68710481 0.09933775]
[0.54972217 0.09602649]
[0.4696302 0.29525386]
[0.50028741 0.48068433]
[0.39662771 0.7781457 ]
[0.46809734 0.424117 ]]↓ epoch을 5000번으로 하고 loss 감소를 지켜봤음
w1, w2, bias = gradient_descent(scaled_features, bostonDF['PRICE'].values, epochs=5000, verbose=True)
print()
print('#' * 15 + ' final weights ' + '#' * 15)
print('w1', w1, 'w2', w2, 'bias', bias)
print('#' * 45)↓ 결과
############### initial weights ###############
w1 [0.] w2 [0.] bias [1.]
###############################################
Epoch : 1 / 5000
w1 [0.24193162] w2 [0.10311943] bias [1.43065613] loss 548.0813043478261
Epoch : 2 / 5000
w1 [0.47767212] w2 [0.20269304] bias [1.84955238] loss 522.964778344195
Epoch : 3 / 5000
w1 [0.70739021] w2 [0.29881838] bias [2.25700994] loss 499.19625820107575
Epoch : 4 / 5000
w1 [0.93124998] w2 [0.39159032] bias [2.65334123] loss 476.7031232605375
Epoch : 5 / 5000
w1 [1.14941104] w2 [0.48110116] bias [3.03885015] loss 455.41666565492966
Epoch : 6 / 5000
w1 [1.36202867] w2 [0.56744065] bias [3.41383227] loss 435.2718794853261
Epoch : 7 / 5000
w1 [1.56925388] w2 [0.65069613] bias [3.7785751] loss 416.20726135905875
Epoch : 8 / 5000
w1 [1.77123356] w2 [0.73095251] bias [4.13335831] loss 398.1646216743121
Epoch : 9 / 5000
w1 [1.96811059] w2 [0.8082924] bias [4.47845392] loss 381.0889060727257
Epoch : 10 / 5000
w1 [2.16002396] w2 [0.88279616] bias [4.81412652] loss 364.9280265121499
...
Epoch : 4991 / 5000
w1 [25.41618171] w2 [-23.59901673] bias [16.3865252] loss 30.52917556908624
Epoch : 4992 / 5000
w1 [25.41645342] w2 [-23.59917839] bias [16.38643161] loss 30.52916468591784
Epoch : 4993 / 5000
w1 [25.41672499] w2 [-23.59933982] bias [16.38633802] loss 30.5291538178668
Epoch : 4994 / 5000
w1 [25.4169964] w2 [-23.59950105] bias [16.38624444] loss 30.52914296490582
Epoch : 4995 / 5000
w1 [25.41726768] w2 [-23.59966205] bias [16.38615088] loss 30.529132127007642
Epoch : 4996 / 5000
w1 [25.41753881] w2 [-23.59982284] bias [16.38605732] loss 30.529121304145082
Epoch : 4997 / 5000
w1 [25.41780979] w2 [-23.59998341] bias [16.38596378] loss 30.529110496290976
Epoch : 4998 / 5000
w1 [25.41808063] w2 [-23.60014377] bias [16.38587025] loss 30.529099703418233
Epoch : 4999 / 5000
w1 [25.41835132] w2 [-23.60030391] bias [16.38577672] loss 30.529088925499806
Epoch : 5000 / 5000
w1 [25.41862187] w2 [-23.60046384] bias [16.38568321] loss 30.52907816250869
############### final weights ###############
w1 [25.41862187] w2 [-23.60046384] bias [16.38568321]
#############################################KERAS 구현
from tensorflow.keras.layers import Dense
from tensorflow.keras.models import Sequential
from tensorflow.keras.optimizers import Adam
model = Sequential([
Dense(units=1, input_shape=(2, ), activation=None, kernel_initializer='zeros', bias_initializer='ones')
])
model.compile(optimizer=Adam(learning_rate=.01), loss='mse', metrics=['mse'])
model.fit(scaled_features, bostonDF['PRICE'].values, epochs=5000)Epoch 1/5000
16/16 [==============================] - 0s 1ms/step - loss: 542.3798 - mse: 542.3798
Epoch 2/5000
16/16 [==============================] - 0s 998us/step - loss: 530.2786 - mse: 530.2786
Epoch 3/5000
16/16 [==============================] - 0s 798us/step - loss: 518.2217 - mse: 518.2217
Epoch 4/5000
16/16 [==============================] - 0s 864us/step - loss: 506.6226 - mse: 506.6226
Epoch 5/5000
16/16 [==============================] - 0s 798us/step - loss: 495.0897 - mse: 495.0897
...
Epoch 4996/5000
16/16 [==============================] - 0s 731us/step - loss: 30.5230 - mse: 30.5230
Epoch 4997/5000
16/16 [==============================] - 0s 798us/step - loss: 30.5204 - mse: 30.5204
Epoch 4998/5000
16/16 [==============================] - 0s 731us/step - loss: 30.5145 - mse: 30.5145
Epoch 4999/5000
16/16 [==============================] - 0s 731us/step - loss: 30.5184 - mse: 30.5184
Epoch 5000/5000
16/16 [==============================] - 0s 731us/step - loss: 30.5188 - mse: 30.5188직접 구현할 때 loss가 30.529였는데 keras 구현 때는 mse loss가 30.519로 조금 떨어졌다
아마 Adam optimizer를 써서 그런지 직접 구현할 때랑 mse가 다르다
keras_pred_price = model.predict(scaled_features)
bostonDF['KERAS_PRED_PRICE'] = keras_pred_price
bostonDF
대충 pred_price랑 keras_pred_price가 비슷하게 나왔다
근데 다 좋은데 keras로 얻은 w1, w2, bias가 얼만지 어떻게 아나요...
'Computer Vision > 딥러닝 CNN 완벽 가이드' 카테고리의 다른 글
| Stochastic Gradient Descent & Mini-Batch Gradient Descent (1) | 2023.02.05 |
|---|---|
| 딥러닝 CNN 완벽 가이드 (권철민) 리뷰 1편 (0) | 2022.12.21 |
출처
딥러닝 CNN 완벽 가이드 - Fundamental 편
딥러닝 CNN 완벽 가이드 - Fundamental 편 - 인프런 | 강의
딥러닝·CNN 핵심 이론부터 다양한 CNN 모델 구현 방법, 실전 문제를 통한 실무 딥러닝 개발 노하우까지, 딥러닝 CNN 기술 전문가로 거듭나고 싶다면 이 강의와 함께하세요 :), - 강의 소개 | 인프런..
www.inflearn.com
이론

mse loss function 그래프에서 점진적인 하강을 통해 local minimum/maximum을 찾아나가는 방식
mse loss function 기울기에 learning_rate를 곱해서 weight/bias를 업데이트함
↑ 각 weight/bias로 편미분해서 기울기를 구함
보스턴 주택 가격 데이터 세트 학습 실습
뉴럴 네트워크 직접 구현
import numpy as np
import pandas as pd
from sklearn.datasets import load_boston
boston = load_boston()
print(boston['feature_names'])['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO' 'B' 'LSTAT']여러 features 중에서 영향력이 제일 큰 RM과 LSTAT만 이용해 예측해 봄
bostonDF = pd.DataFrame(data=boston['data'], columns=boston['feature_names'])
bostonDF['PRICE'] = boston['target']
bostonDF
↓ 뉴럴 네트워크 구조

↓ Gradient Descent 원리

↓ weight/bias update value 구하는 함수 구현
def get_descent_values(w1, w2, bias, rm, lstat, price, learning_rate=.01):
N = len(price)
pred = w1 * rm + w2 * lstat + bias
diff = price - pred
dw1 = learning_rate * (2 / N) * (diff @ rm)
dw2 = learning_rate * (2 / N) * (diff @ lstat)
db = learning_rate * (2 / N) * sum(diff)
loss = np.mean(np.square(diff))
return dw1, dw2, db, loss↑ 여기서 rm, lstat, price는 모두 1차원 배열 형태로 입력될 예정
↓ 드디어 gradient descent 구현하는 함수
def gradient_descent(features, price, epochs, verbose=True):
w1 = np.zeros((1,))
w2 = np.zeros((1,))
bias = np.ones((1,))
print('#' * 15 + ' initial weights ' + '#' * 15)
print('w1', w1, 'w2', w2, 'bias', bias)
print('#' * 47)
print()
learning_rate = .01
rm = features[:, 0]
lstat = features[:, 1]
for i in range(epochs):
dw1, dw2, db, loss = get_descent_values(w1, w2, bias, rm, lstat, price, learning_rate)
w1 += dw1
w2 += dw2
bias += db
if verbose:
print('Epoch :', i + 1, '/', epochs)
print('w1', w1, 'w2', w2, 'bias', bias, 'loss', loss)
return w1, w2, bias데이터에 preprocessing이 필요함
↓ 보통 데이터를 0에서 1 사이로 정규화해 놓는 게 좋음
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaled_features = scaler.fit_transform(bostonDF[['RM', 'LSTAT']])
print(scaled_features[:10])[[0.57750527 0.08967991]
[0.5479977 0.2044702 ]
[0.6943859 0.06346578]
[0.65855528 0.03338852]
[0.68710481 0.09933775]
[0.54972217 0.09602649]
[0.4696302 0.29525386]
[0.50028741 0.48068433]
[0.39662771 0.7781457 ]
[0.46809734 0.424117 ]]↓ epoch을 5000번으로 하고 loss 감소를 지켜봤음
w1, w2, bias = gradient_descent(scaled_features, bostonDF['PRICE'].values, epochs=5000, verbose=True)
print()
print('#' * 15 + ' final weights ' + '#' * 15)
print('w1', w1, 'w2', w2, 'bias', bias)
print('#' * 45)↓ 결과
############### initial weights ###############
w1 [0.] w2 [0.] bias [1.]
###############################################
Epoch : 1 / 5000
w1 [0.24193162] w2 [0.10311943] bias [1.43065613] loss 548.0813043478261
Epoch : 2 / 5000
w1 [0.47767212] w2 [0.20269304] bias [1.84955238] loss 522.964778344195
Epoch : 3 / 5000
w1 [0.70739021] w2 [0.29881838] bias [2.25700994] loss 499.19625820107575
Epoch : 4 / 5000
w1 [0.93124998] w2 [0.39159032] bias [2.65334123] loss 476.7031232605375
Epoch : 5 / 5000
w1 [1.14941104] w2 [0.48110116] bias [3.03885015] loss 455.41666565492966
Epoch : 6 / 5000
w1 [1.36202867] w2 [0.56744065] bias [3.41383227] loss 435.2718794853261
Epoch : 7 / 5000
w1 [1.56925388] w2 [0.65069613] bias [3.7785751] loss 416.20726135905875
Epoch : 8 / 5000
w1 [1.77123356] w2 [0.73095251] bias [4.13335831] loss 398.1646216743121
Epoch : 9 / 5000
w1 [1.96811059] w2 [0.8082924] bias [4.47845392] loss 381.0889060727257
Epoch : 10 / 5000
w1 [2.16002396] w2 [0.88279616] bias [4.81412652] loss 364.9280265121499
...
Epoch : 4991 / 5000
w1 [25.41618171] w2 [-23.59901673] bias [16.3865252] loss 30.52917556908624
Epoch : 4992 / 5000
w1 [25.41645342] w2 [-23.59917839] bias [16.38643161] loss 30.52916468591784
Epoch : 4993 / 5000
w1 [25.41672499] w2 [-23.59933982] bias [16.38633802] loss 30.5291538178668
Epoch : 4994 / 5000
w1 [25.4169964] w2 [-23.59950105] bias [16.38624444] loss 30.52914296490582
Epoch : 4995 / 5000
w1 [25.41726768] w2 [-23.59966205] bias [16.38615088] loss 30.529132127007642
Epoch : 4996 / 5000
w1 [25.41753881] w2 [-23.59982284] bias [16.38605732] loss 30.529121304145082
Epoch : 4997 / 5000
w1 [25.41780979] w2 [-23.59998341] bias [16.38596378] loss 30.529110496290976
Epoch : 4998 / 5000
w1 [25.41808063] w2 [-23.60014377] bias [16.38587025] loss 30.529099703418233
Epoch : 4999 / 5000
w1 [25.41835132] w2 [-23.60030391] bias [16.38577672] loss 30.529088925499806
Epoch : 5000 / 5000
w1 [25.41862187] w2 [-23.60046384] bias [16.38568321] loss 30.52907816250869
############### final weights ###############
w1 [25.41862187] w2 [-23.60046384] bias [16.38568321]
#############################################KERAS 구현
from tensorflow.keras.layers import Dense
from tensorflow.keras.models import Sequential
from tensorflow.keras.optimizers import Adam
model = Sequential([
Dense(units=1, input_shape=(2, ), activation=None, kernel_initializer='zeros', bias_initializer='ones')
])
model.compile(optimizer=Adam(learning_rate=.01), loss='mse', metrics=['mse'])
model.fit(scaled_features, bostonDF['PRICE'].values, epochs=5000)Epoch 1/5000
16/16 [==============================] - 0s 1ms/step - loss: 542.3798 - mse: 542.3798
Epoch 2/5000
16/16 [==============================] - 0s 998us/step - loss: 530.2786 - mse: 530.2786
Epoch 3/5000
16/16 [==============================] - 0s 798us/step - loss: 518.2217 - mse: 518.2217
Epoch 4/5000
16/16 [==============================] - 0s 864us/step - loss: 506.6226 - mse: 506.6226
Epoch 5/5000
16/16 [==============================] - 0s 798us/step - loss: 495.0897 - mse: 495.0897
...
Epoch 4996/5000
16/16 [==============================] - 0s 731us/step - loss: 30.5230 - mse: 30.5230
Epoch 4997/5000
16/16 [==============================] - 0s 798us/step - loss: 30.5204 - mse: 30.5204
Epoch 4998/5000
16/16 [==============================] - 0s 731us/step - loss: 30.5145 - mse: 30.5145
Epoch 4999/5000
16/16 [==============================] - 0s 731us/step - loss: 30.5184 - mse: 30.5184
Epoch 5000/5000
16/16 [==============================] - 0s 731us/step - loss: 30.5188 - mse: 30.5188직접 구현할 때 loss가 30.529였는데 keras 구현 때는 mse loss가 30.519로 조금 떨어졌다
아마 Adam optimizer를 써서 그런지 직접 구현할 때랑 mse가 다르다
keras_pred_price = model.predict(scaled_features)
bostonDF['KERAS_PRED_PRICE'] = keras_pred_price
bostonDF
대충 pred_price랑 keras_pred_price가 비슷하게 나왔다
근데 다 좋은데 keras로 얻은 w1, w2, bias가 얼만지 어떻게 아나요...
'Computer Vision > 딥러닝 CNN 완벽 가이드' 카테고리의 다른 글
| Stochastic Gradient Descent & Mini-Batch Gradient Descent (1) | 2023.02.05 |
|---|---|
| 딥러닝 CNN 완벽 가이드 (권철민) 리뷰 1편 (0) | 2022.12.21 |
